This is a simple solar collector being used to warm water. We get cool water entering the solar collector and warm water leaving it.

If we look at the interior of it we see that the pipe snakes back and forth throughout the collector collecting as much solar energy as we can. We're going to neglect any heat losses from the sides and the bottom of this collector and are really just gonna focus on the top of the collector and see how much sunlight is being absorbed.

So to do that, let's take a look at our solar collector from the side, here we've provided relevant temperatures; the temperature of the sun, the temperature of the sky above ambient temperature in the local vicinity of the plate, and the surface temperature of the plate itself. The area of the plate has the dimensions of one meter by one meter, so the area is one square meter.

So the primary means at which the plate gathers energy is from the sun itself. So there's some solar insulation, G, and only a fraction of that radiation actually is absorbed by the plate. So to account for that we're gonna multiply by the plate's absorptivity. In doing so, we can now neglect the amount of reflected radiation because it's all being accounted for in alpha. We might incorrectly assume that G is equal to sigma times the temperature of the sun to the fourth power. And in doing so, we would predict that the plate receives 63 megawatts of energy per square meter.
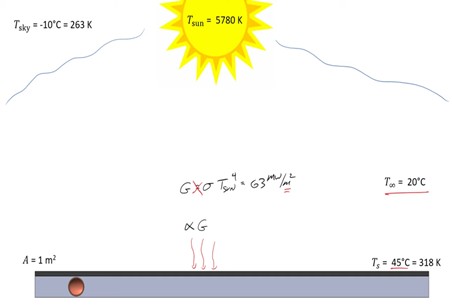
Of course, we're not at the surface of the sun, that's what this meter squared represents, the meter squared of the surface of the sun. If we were, we would burn our plate up, so that is not a reasonable value for the amount of irradiation from the sun, because we're so far away from the sun. The more reasonable value is 900 watts per square meter. Multiply that by the area, and we find that the sun shines about 900 watts of energy on the surface of the plate.
We also have irradiation from the sky and the sky is relatively cool and we can represent that as the absorptivity multiplied by sigma times T-sky to the fourth power. We also have energy loss in the form of diffuse radiation from the surface of the plate. It means the radiation comes off uniformly in all directions from the plate. So to calculate this, we'll say the emissivity of the plate multiplied by sigma times surface temperature to the fourth power. We've also got natural convection coming off the surface of the plate, using appropriate correlation for natural convection from a plate. We find that ℏ is about equal to 4.7 watts per square meter cal.
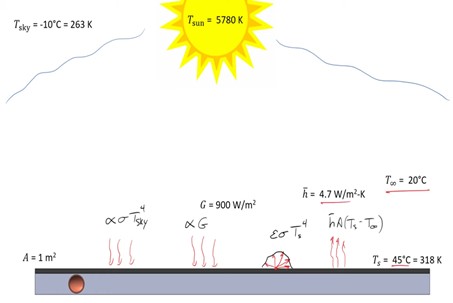
So we find out the amount of energy being transferred from the water is due to irradiation from both the sky and the sun minus the loss due to natural convection and radiation out into the surroundings. If we were to assume that the surface was perfectly black we would find that the absorptivity and the emissivity were all equal to one and now it becomes a matter of plugging in numbers to find the solution.
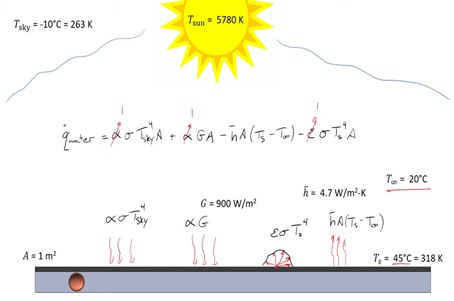
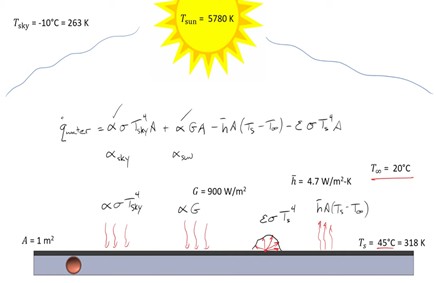
However, to complicate matters, it turns out the surface is not black, and in fact, the values of alpha, these two values are not the same. So we’re gonna call one alpha-sky and another alpha-sun. They aren't the same and we need to go about calculating them.
To be able to do that we first have to talk about what it means for a surface to be black or gray or semi gray. In the graph below, the spectral emissivity and the spectral absorptivity for the three types of surfaces are shown, and due to Kirchhoff's law, we find that the spectral emissivity and the spectral absorptivity will be equal in all cases because the radiation is diffuse. At the top is what's known as a black surface which means it absorbs 100% of the radiation for all values of λ for all wavelengths of radiation. The second surface is known as a gray surface and the value of ε and alpha are the same value for all values of λ and they're less than a hundred percent but the idea behind a gray surface is that ε and alpha are the same for all wavelengths. And in the third case is what's known as a semi-gray surface. Again, the value of ε and alpha and in this case the spectral emissivity and the spectral absorptivity are different values for different wavelengths. We're going to say that there's a step change either downward or upward at some critical value of λ. We'll call that some value λ-critical. And in this case, we’ve set λ-critical equal to five microns, and we've said the spectral emissivity and the spectral absorptivity are equal to 0.9 at short wavelengths and equal to 0.1 at longer wavelengths.
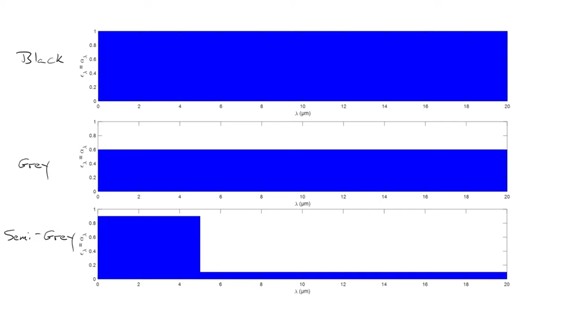
Recall that if the surface was black, we could have completed the problem by now because we would've set ε and alpha equal to one in all cases. If the surface was gray, we could have simply set ε and alpha equal to 0.6 in all cases, however, the surface we're dealing with here is semi gray, so the question becomes, well, what is ε itself or what is alpha itself? Because the wavelengths from the sun tend to be very short and the wavelengths of the emitting surface tend to be longer because the temperature of the surface is of course much cooler than the surface of the sun.
Here is a simulation of a gray surface in which the spectral emissivity and the spectral absorptivity are equal to 0.6 for all values of λ. And I'm keeping the temperature right now at the temperature of the sun. We see most of the energy occurs at short wavelengths.
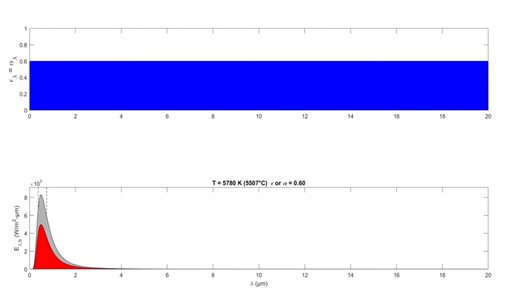
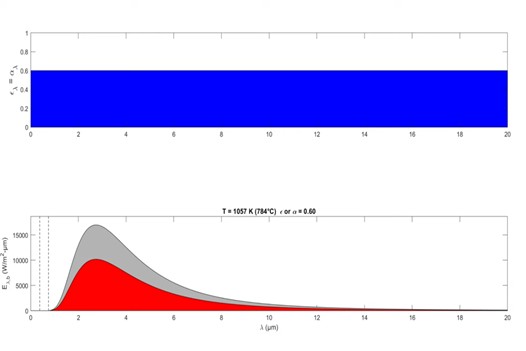
However, if we take the surface and cool it down, we see a shift to higher and higher wavelengths. It's scaling by orders of magnitude as we decrease the temperature. So if we move from right to left, the temperature increases and the energy increases by orders of magnitude. The gray curve represents the emission if this was a black body and the red curve represents the case in which we have a gray surface in which we've set the emissivity equal to 60% across the board for all temperatures,which means that the area under the red curve is exactly 60% of the area under the gray curve.
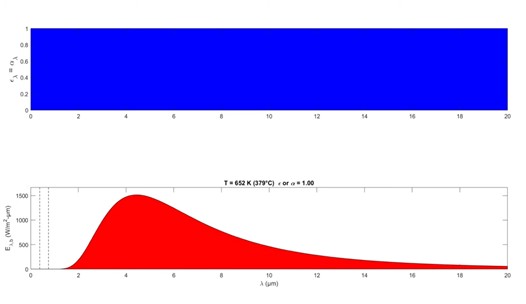
This next simulation shows what would occur if the surface was black, we would find that the area under the red curve is exactly equal to the area under the gray curve because the surface is black. So in this case, ε and alpha are equal to a hundred percent no matter what the temperature is, even for the cool temperature of the plate it's equal to one and the temperature of the sun, it's also equal to one.
For the case of the semi gray surface however, we'll find that the area of the red curve is 90% of the area of the gray curve at short wavelength.
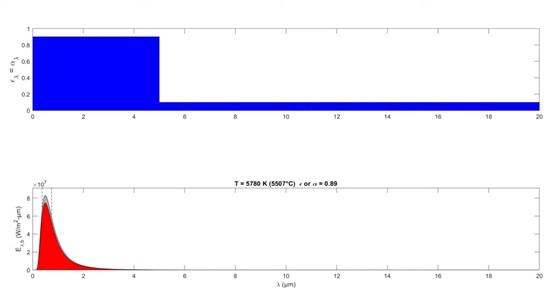
What we find is that as we decrease the temperature the fraction of radiation being emitted or being absorbed above five microns is substantially less that we find the right of that critical value of λ, the actual radiative power is only 10% of that of the black body and to the left it's only 90%. So we have to figure out what value of ε and what value of alpha to use, which is indicated on the title on the bottom. So what we find, if we increase the temperature back up to the temperature of the sun, we see ε and alpha are about equal to 90%, almost equal to 90%, very little of the radiation coming from the sun has wavelengths longer than five microns
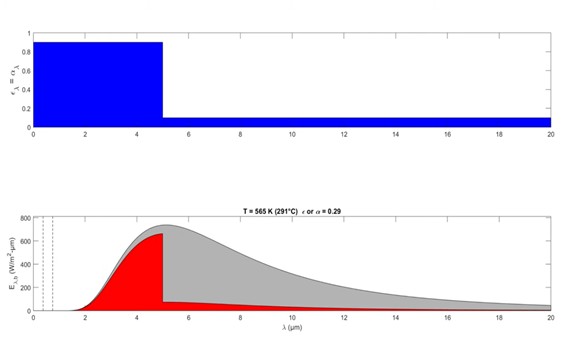
As we cool it down though we're gonna continue cooling this down, pay attention to ε and alpha it's now at 68% at a temperature of 889° C. We're gonna continue cooling this down until we hit the temperature of the plate, which is at a temperature of 45° C. ε and alpha are at 0.12 at the temperature of the sky equal to minus 10° C, which is very cold.
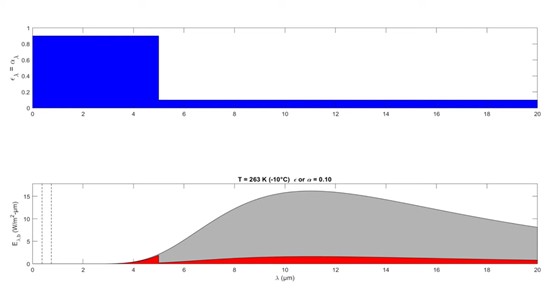
If we were to continue to go even colder than that we would find that little or no radiation occurs at wavelength shorter than five microns. So at this temperature it would be safe to say that we were dealing with a gray surface because the step change in the spectral emissivity doesn't affect it.
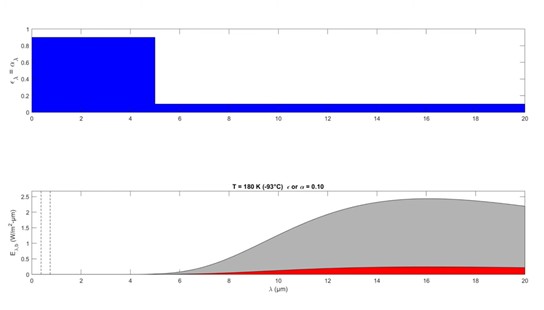
If we'll heat this back up again. We'll find the emissivity and the absorptivity are approaching 90% at the temperature of the sun. So for the temperature of the sun, we'd say alpha-sun was equal to 0.89, for the surface temperature of 45° we'll use ε equal to 0.12, and for the sky we're going to use an absorptivity of 10%. So those are the numbers we're going to plug in to figure out the heat being delivered to the water.
We'll first note that the area under the red curve is the actual emissive power. The area under the gray curve is equal to the black body emissive power which is equal to sigma times T to the fourth. And the ratio of those two, E divided by sigma T to the fourth is equal to the value of ε that we're going to use. And in this case we've got the temperature 45° for the surface. Formally we'd write this, the value of ease being the integral of the red curve which isn't necessarily easy to integrate. So what we did was split it into two parts. We've got a part with ε one which is 90% and ε two, which is equal to 10%. And the fact that those are constants means that I can pull these out of both of those integrals.
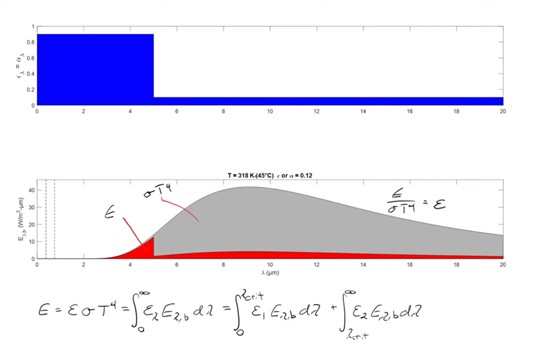
So here we've rearranged those and solved for the value of ε that we wish to use. Now the tricky part is evaluating these integrals because we need to evaluate the integral of this function which isn't easy to do, there's no analytical expression for it. So what we did in our simulations was we used an ODE solver in MATLAB. Alternatively, we can recognize that this represents the fraction of the black body emissive power that occurs below our critical value of λ. And the term on the right represents the fraction of the black body emissive power that occurs above the critical value of λ.
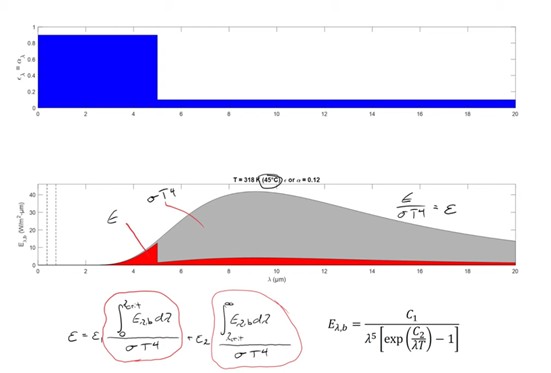
Here we've represented the first integral as a fraction that is tabulated which we could look up. And the second integral is one minus the original fraction which we could look up, and because we know the temperature of the solar collectors is equal to 45°, we can find that its emissivity is equal to 0.12.
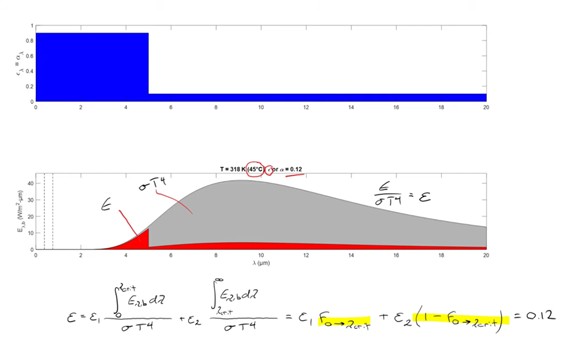
To go back to the original problem we find that alpha-sky is about equal to 0.104, we find that alpha-sun, because it's wavelengths were so short we find that that value is equal to 0.896 and we find the emissivity from the solar collector was equal to 0.115. Plugging in all of these numbers, we find that the amount of heat added to the water is about equal to 650 watts. Note that 900 watts of solar energy is being delivered to the surface, so we could find an efficiency of 650 divided by 900, which is equal to 72%. So 72% of the sunlight is being delivered to the water.


Please give us a message
DINGXIN story
One electric water heater branded as Dingxin, which has warmed Mr Chen for 22 years. In 1991,Mr Chen bought a new water heater and normally lived with it as long as 22 years in Wenzhou
The Family business
DINXIN ADVENTURE THROUGH 2 GENERATIONS, FROM THE START IN 1986 TO TODAY.
The family business
The founder –Dong Wanwen– started “Dingxin” (in Wenzhou in 1986, as one of the first water heater manufacture in China. With minimal resources he created the first vented water heater in Wenzhou. He has, during his 30 years in Dingxin, mixed friendly industry and home culture in a unique way and has given Dingxin the recognition as one of the earliest enterprises in china.
2rd generation –Eric Dong,is devoted to improving Dingxin’s products and processes and desires to build the company brick by brick,. The pioneering spirit lives on with product innovations featuring integrated solutions, ground-breaking material technology and added value for our customers.
Three main markets oriention of Dingxin:
• Northern China: Thanks to trust and confidence from our customers, Dingxin engages a attractive market share in North China over the last 30 years. Our products named as Dignxin delivers well-being and hotwater to two-thirds of all homes in the three north-east of provinces of china, with durable lifetime economy.
• OEM/EXPORT: We are proud to supply water heaters to various brands in the heating industry all over Europe,South America,South asia. OEM is an important part of our business because it inspires and motivates us to think innovatively, be flexible in our approach and challenge traditional mind-sets.
• Kitchen&bathroom branch: Dingxin focuses on the domestic market of kitchen&bathroom since 2016 and whose sales make up about 40% of the turnover and gives us a unique perspective and knowledge of related business lines and innovative marketing strategies which benefit all our customers.
DINGXIN story
One electric water heater branded as Dingxin, which has warmed Mr Chen for 22 years. In 1991,Mr Chen bought a new water heater and normally lived with it as long as 22 years in Wenzhou
Historic milestones
Dingxin launched a promise to replace the water heaters free of charge for those were purchased before 1995 and still normally used up to 2015. When Mr. Zhang saw this news,he immediately rushed to the Dingxin franchise shop of department store in Taiyuan city, Shanxi province. the Dingxin staff there offered Mr. Zhang for a free replacement service;
One electric water heater branded as Dingxin, which has warmed Mr Chen for 22 years. In 1991,Mr Chen bought a new water heater and normally lived with it as long as 22 years in Wenzhou .when Dingxin launched a campaign that every home could receive new water heater replacement installation service free of charge only if who purchased Dinxin water heaters before 1995 and still normally adopt it with over 22 years, Surely Mr Chen belongs to the ones who could received this fantastic service launched by Dingxin.
Mr. Zhu, in Dingxin franchise department, purchased two electric water heaters in 1988 and he spent ¥500 in all. When it comes to 2014, the two electric water heaters have been in its life time for 26 years and still have been in fantastic condition. The Dingxin promise to offer free replacement service of the two water heaters
In 1993, Mr. Wang purchased this water heater in franchise department of Tangshan city, Hebei province.and it is well in circulation for over 23 years, Dingxin offer free replacement service out of security considerations in 2015
Warranty Information
Dingxin warrants for 2 years from the date of purchase, that the Product will: i) conform to Dingxin approval specification, ii) be free from defects in materials and workmanship, subject to conditions below. All electric components carry a 2-year warranty
Scope
Dingxin warrants for 2 years from the date of purchase, that the Product will: i) conform to Dingxin approval specification, ii) be free from defects in materials and workmanship, subject to conditions below. All electric components carry a 2-year warranty.
The warranty is voluntarily extended by Dingxin to 5 years for the premium models. This extended warranty only applies to Products purchased by a consumer, that has been installed for private use and that has been distributed by Dingxin or by a distributor where the Products have been originally sold by Dingxin.
The extended warranty does not apply to Products purchased by commercial entities or for Products that have been installed for commercial use. These shall be subject only to the mandatory provisions of the law. The conditions and limitations set out below shall apply.
Warranty Information
Dingxin warrants for 2 years from the date of purchase, that the Product will: i) conform to Dingxin approval specification, ii) be free from defects in materials and workmanship, subject to conditions below. All electric components carry a 2-year warranty
Coverage
If a defect arises and a valid claim is received within the statutory warranty period, at its option and to the extent permitted by law, Dingxin shall either; i) repair the defect, or; ii) replace the product with a product that is identical or similar in function, or; iii) refund the purchase price.
Dingxin possess all property of any exchanged Product or component. Any valid claim or service does not extend the original warranty. The replacement received Product or part does not carry a new warranty.
Manufacturing
Excellent working condition & longer service life: no leakage, rust-free, high strength and strong resistance to corrosion
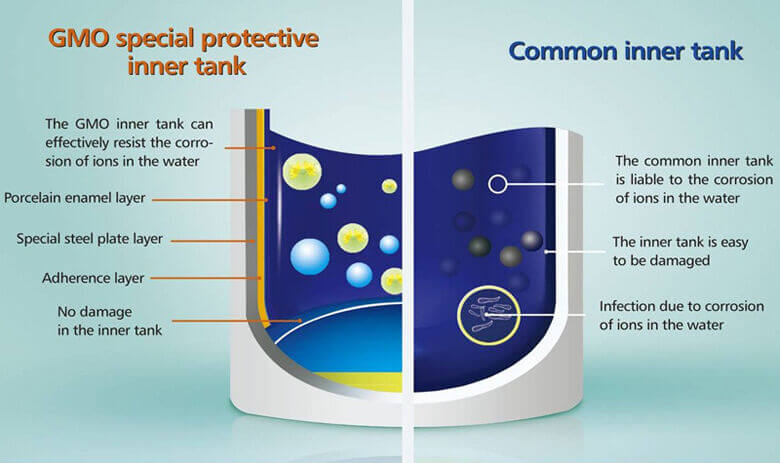
Tank comparison
COMPARISION BETWEEN SS TANK AND ENAMEL TANK
ENAMEL TANK
Porcelain Enamel Tank - is a trusted & proven technology for inner tank of water heaters. Used widely across the world, it is ideal for long life & trouble free performance in all kinds of water. More than 95% of water heaters produced worldwide are with enamel tanks. Corrosion protection is very good due to fusion of glass layer to metal.
SS TANK
Stainless Steel Tank - this is an outdated technology that manufacturers are moving out of now. Corrosion protection is very poor, particularly in hard water and due to poor welding quality.
SL Description Enamel Tank SS Tank
1 Protection Coating Porcelain Enamel -
2 Coating Type Inorganic None
3 Coating Thickness 250 - 400 microns None
4 Coating Adhesion Fused with metal None
5 Baking Temperature 850 deg C -
6 Life of the Coating Long life -
7 Usage Widely used Internationally Limited. In very few countries
8 Material Mild Steel Stainless Steel
9 Thickness 2.0mm 0.63
10 Rated Pressure 8kg/cm2 3kg/cm2 & 6kg/cm2
11 cathodic protection Magnesium Anode -
12 Hard water Suitability Good Poor
13 Corrosion Protection V.Good Poor-Average
14 Hot Water resistant V.Good V.Good
15 Approved Quality Standards BIS, IEC, DIN & UL BIS
HARD WATRT
As so common problem for millions of households across the country.Hard water means excessive dissolved minerals, specifically calcium and magnesium in tap water various in different countries.
Hard water is a negative impact because of much limescale it brings, Thus, in water heaters the heated hard water forms a scale of limescale deposits on the tank surface and reduces the heat conductivity of heaters sometimes even leading to its breakdown. and this contributes to inefficiency and costly electricity bill . Limescale has been known to increase energy bills by up to 25%.
Efficiency loss chart(limes scale thickness as variable)
Manufacturing
Excellent working condition & longer service life: no leakage, rust-free, high strength and strong resistance to corrosion
Water heater tank
Advantage of Enamel coating water tank:
1. Excellent working condition & longer service life: no leakage, rust-free, high strength and strong resistance to corrosion。
2. Clean energy and green product: no poisonous metal such as plumbum, hydrargyrum and chromium, bring health to your life。
3. Do good to heat preservation
1. Excellent working condition & longer service life
2. Clean energy and green product
3. Do good to heat preservation
Workmanship of enamel water tank:
1. High-strength low-carbon steel plate
2. Ultra-fine powder enamel layer
3. Blue high-temperature calcination coating
4. Three-layer strengthened protection
5. No deformation under 100,000 times impulse test

Downloads
Excellent working condition & longer service life: no leakage, rust-free, high strength and strong resistance to corrosion
Installation and manuals
Downloads
Excellent working condition & longer service life: no leakage, rust-free, high strength and strong resistance to corrosion
Product Catalogue
- Exporting Electric Water Heaters to Africa: Market Insights and Strategies
- Small-Capacity Electric Water Heaters in Africa: Market Preferences Across Key Countries
- How to know the quality of stainless steel electric heating element?
- What are the basic structures of stainless steel electric heating element?
- Let's Take A Look At The Inner Tank Material!
Warranty Information
Dingxin warrants for 2 years from the date of purchase, that the Product will: i) conform to Dingxin approval specification, ii) be free from defects in materials and workmanship, subject to conditions below. All electric components carry a 2-year warranty
Conditions
The Product is manufactured to suit most household water supplies. However, there are certain water chemistries (outlined below) that can have a detrimental effect on the Product and its life expectancy. If there are uncertainties regarding water quality, the local water supply authority can supply the necessary data. The warranty applies only if the conditions set out below are met in full:
• The Product has been installed by a professional installer, in accordance with the instructions in the installation manual and all relevant Codes of Practice and Regulations in force at the time of installation.
• The Product has not been modified in any way, tampered with or subjected to misuse and no factory fitted parts have been removed for unauthorized.
• Any disinfection has been carried out without affecting the Product in any way whatsoever. The Product shall be isolated from any system chlorination.
• The Product has been in regular use from the date of installation. If the Product is not intended to be used for 60 days or more, it must be drained.
• Service and/or repair shall be done according to the installation manual and all relevant codes of practice. Any replacement parts used shall be original DINGXIN i spare parts.
• Any third-party costs associated with any claim has been authorized in advance by DINGXIN in writing.
• The purchase invoice and/or installation invoice, a water sample as well as the defective product is made available to DINGXIN i upon request.
• Failure to follow these instructions and conditions may result in product failure, and water escaping from the Product.
Warranty Information
Dingxin warrants for 2 years from the date of purchase, that the Product will: i) conform to Dingxin approval specification, ii) be free from defects in materials and workmanship, subject to conditions below. All electric components carry a 2-year warranty
Limitations
The warranty does not cover:
• Any fault or costs arising from incorrect installation, incorrect application, lack of regular maintenance in accordance with the installation manual, neglect, accidental or malicious damage, misuse, any alteration, tampering or repair carried out by a non-professional, any fault arising from the tampering with or removal of any factory fitted safety components or measures.
• Any consequential damage or any indirect loss caused by any failure or malfunction of the Product whatsoever.
• Any pipework or any equipment connected to the Product.
• The effects of frost, lightning, voltage variation, lack of water, dry boiling, excess pressure or chlorination procedures.
• The effects of stagnant (de-aerated) water if the Product has been left unused for more than 60 days consecutively.
• Damage caused during transportation. Buyer shall give the carrier notice of such damage.
• Costs arising if the Product is not immediately accessible for servicing.
These warranties do not affect the Buyer’s statutory rights.
FAQ
Q1:How long does the order take?
A:Sample order will be finished within 15 days while normal order will be finished within 25-30 days after receiving deposit,
Q2:What are my WARRANTY OPTIONS on the water heaters you sell?
Dingxin Water Heater Company provides a basic, standard warranty. Our basic warranty is one year for full units or 1% spare parts service.
Q3:Do you accept OEM or ODM orders?
A:Yes, Our R&D team will offer one stop service for you from original idea to finished product.
Q4:What’s the MOQ?
A: Normally MOQ is 1*20 ft container(trial order's quantity is negotiable)
Q5:How can I visit your factory?
A: Sure,Our factory is located in Shaoxing Shengzhou, China, near to Hangzhou Airport and Ningbo Airport .You are always welcome to visit us! We will offer pick up service and free accomodation.
Q6:When can I get the price?
A:Within 24 hours after we get your inquiry.
Q7:Can you offer sample for quality check before order ?
A:Yes , we provide sample service before mass order.
Q8: what other size water heater you have ?
A: We have storage models of 8L\10L\15L\30L\50L\60L\80L\100L\120L\150L,and besides storage model,we also work on instant models,and gas models.
Q9: Can the price be cheaper?
A: Price always follows its quality and we will offer truthful opinion on the marketing strategy on pricing and quality orientation.
Q10: What payment terms?
A: T/T; L/C,West Union or other payment term negotiable
Please give us a message
